Quantum Computing in Action

Transforming Industries Through Quantum Power

Quantum computing is rapidly emerging as a transformative force across multiple sectors, leveraging the principles of quantum mechanics to solve previously intractable problems. In finance, quantum algorithms are revolutionizing portfolio optimization and risk analysis, with quantum annealing techniques solving complex optimization problems in minutes rather than days. The pharmaceutical industry is experiencing a paradigm shift in drug discovery, as quantum simulations of molecular interactions, powered by variational quantum eigensolver (VQE) algorithms, dramatically accelerate the identification of new therapeutic compounds. Similarly, in logistics, quantum-optimized routing solutions are significantly reducing fuel consumption and delivery times, while in climate science, quantum-enhanced models are improving the accuracy of long-term predictions crucial for environmental policy-making.

The impact of quantum computing extends further, touching fields as diverse as cybersecurity, artificial intelligence, and materials science. Quantum key distribution (QKD) is setting new standards in secure communication, while quantum machine learning algorithms are pushing the boundaries of pattern recognition and data classification. In energy and manufacturing, quantum simulations are accelerating the discovery of new materials for more efficient solar cells and enabling the design of stronger, lighter components with reduced material usage. As quantum hardware continues to advance and algorithms become more sophisticated, we can expect even more profound transformations across these and other sectors, driving innovation, efficiency, and scientific discovery to unprecedented levels. The quantum revolution is not just about incremental improvements; it's about reimagining entire industries and unlocking new realms of possibility.

A Technical Overview

At the heart of quantum computing lies the quantum bit, or qubit, which fundamentally differs from classical bits. While a classical bit can be in one of two states (0 or 1), a qubit can exist in a superposition of states, represented mathematically as |ψ⟩ = α|0⟩ + β|1⟩, where α and β are complex numbers satisfying |α|² + |β|² = 1. This property of superposition, along with quantum entanglement—a phenomenon where qubits become correlated in ways that have no classical counterpart—enables quantum computers to perform certain calculations exponentially faster than classical computers. Quantum gates, the building blocks of quantum circuits, manipulate these qubits through operations like the Hadamard gate (H), which creates superposition, and the Controlled-NOT (CNOT) gate, which entangles qubits. These operations, combined with measurement, form the basis of quantum algorithms that exploit quantum parallelism to solve complex problems efficiently.

The power of quantum computing is harnessed through various quantum algorithms, each designed to address specific types of problems. Shor's algorithm, for instance, offers exponential speedup for integer factorization and discrete logarithms, posing significant implications for cryptography. Grover's algorithm provides quadratic speedup for unstructured search problems, while the Quantum Fourier Transform (QFT) serves as a crucial subroutine in many quantum algorithms, offering efficient implementation of the discrete Fourier transform. More recent developments include the Variational Quantum Eigensolver (VQE) and the Quantum Approximate Optimization Algorithm (QAOA), which are hybrid quantum-classical algorithms suited for near-term quantum hardware. These algorithms operate on quantum circuits implemented on various physical platforms, including superconducting qubits, trapped ions, and photonic systems, each with its own advantages and challenges in terms of coherence time, gate fidelity, and scalability. As the field progresses, quantum error correction techniques, such as surface codes, are being developed to create logical qubits from many physical qubits, aiming to achieve fault-tolerant quantum computation and pave the way for large-scale, practical quantum computers.

Quantum Bits (Qubits)

Quantum bits, or qubits, are the fundamental units of information in quantum computing, analogous to classical bits in conventional computers. However, qubits possess unique properties that set them apart from their classical counterparts. While a classical bit can only be in one of two states, typically represented as 0 or 1, a qubit can exist in a superposition of states, mathematically described as |ψ⟩ = α|0⟩ + β|1⟩, where α and β are complex numbers satisfying the normalization condition |α|² + |β|² = 1. This superposition principle allows a qubit to hold much more information than a classical bit. The state of a qubit can be visualized using the Bloch sphere, where the north and south poles represent the classical |0⟩ and |1⟩ states, respectively, and any point on the surface of the sphere represents a valid qubit state. This geometric representation helps in understanding qubit manipulations and quantum gates, which can be viewed as rotations on the Bloch sphere.

Another crucial property of qubits is quantum entanglement, a phenomenon where two or more qubits become correlated in such a way that the quantum state of each qubit cannot be described independently, even when separated by large distances. This non-local correlation is a key resource in many quantum algorithms and protocols. Physically, qubits can be realized in various systems, including superconducting circuits, trapped ions, photons, and quantum dots, each with its own advantages and challenges in terms of coherence time, gate fidelity, and scalability. The coherence time, which is the duration a qubit can maintain its quantum state before environmental interactions cause it to decohere, is a critical factor in the performance of quantum computers. As qubits interact with their environment, they lose their quantum properties through a process called decoherence, which is one of the main obstacles in building large-scale quantum computers. Ongoing research focuses on improving qubit quality, increasing coherence times, and developing error correction techniques to create logical qubits from many physical qubits, paving the way for fault-tolerant quantum computation.

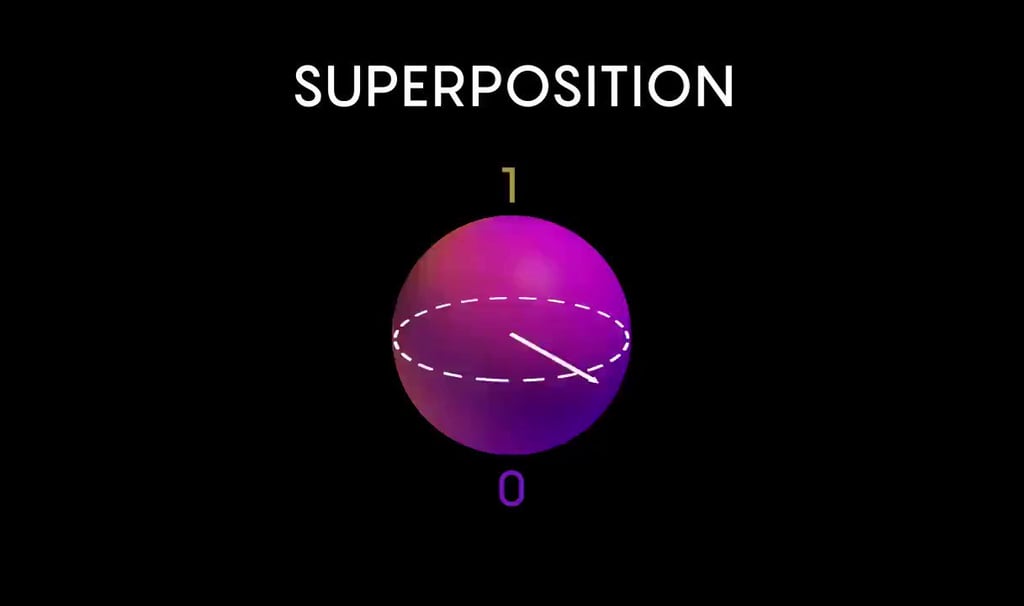
Quantum Superposition

Quantum superposition is a fundamental principle of quantum mechanics that lies at the heart of quantum computing's power. In classical systems, an object must be in one definite state at any given time – for instance, a classical bit is either 0 or 1. However, quantum superposition allows a quantum system to exist in multiple states simultaneously. For a qubit, this means it can be in a combination of both 0 and 1 states at the same time, represented mathematically as |ψ⟩ = α|0⟩ + β|1⟩, where α and β are complex numbers called probability amplitudes. The squares of these amplitudes, |α|² and |β|², give the probabilities of measuring the qubit in the |0⟩ or |1⟩ state respectively. This property enables quantum computers to process multiple possibilities simultaneously, leading to the quantum parallelism that gives quantum algorithms their speed advantage for certain problems.

The concept of superposition extends beyond single qubits to multi-qubit systems, where it becomes even more powerful. In a system of n qubits, superposition allows the quantum state to be a combination of all 2^n possible classical bit strings simultaneously. This exponential growth in the state space is what gives quantum computers their immense computational potential. However, it's crucial to understand that while a quantum system in superposition contains information about all possible states, we can't access all this information directly. When we measure a quantum system, it collapses into one of its basis states, with the probability determined by the amplitudes in the superposition. This measurement problem is at the core of many quantum algorithms, which are designed to manipulate superpositions in ways that increase the probability of measuring the desired result. Techniques like quantum interference and phase kickback are used to amplify the amplitudes of correct solutions while suppressing incorrect ones, allowing quantum algorithms to solve certain problems exponentially faster than classical algorithms.

Quantum Entanglement

Quantum entanglement is a phenomenon in quantum physics where two or more particles become correlated in such a way that the quantum state of each particle cannot be described independently, even when separated by large distances. This "spooky action at a distance," as Einstein famously called it, is a cornerstone of quantum mechanics and a crucial resource in quantum computing and quantum information. In a simple two-qubit system, an entangled state could be represented as |ψ⟩ = (1/√2)(|00⟩ + |11⟩), known as a Bell state. In this state, measuring one qubit immediately determines the state of the other, regardless of the distance between them. This non-local correlation is stronger than any classical correlation and violates the principle of local realism, as demonstrated by the violation of Bell's inequalities in numerous experiments.

Entanglement plays a vital role in many quantum computing algorithms and protocols. In quantum teleportation, entanglement allows the transfer of quantum information without physically transmitting the qubit itself. Superdense coding uses entanglement to transmit two classical bits of information by manipulating and sending only one qubit of an entangled pair. In quantum computing, entanglement is essential for creating multi-qubit gates, such as the CNOT (Controlled-NOT) gate, which are fundamental building blocks of quantum circuits. The ability to create and manipulate entangled states is crucial for achieving quantum advantage in algorithms like Shor's factoring algorithm and quantum simulation of many-body systems. However, maintaining entanglement is challenging due to decoherence, where interactions with the environment cause quantum states to lose their coherence and entanglement. Overcoming this challenge is one of the primary focuses in the development of practical quantum computers, involving techniques such as error correction codes and the creation of topologically protected qubits.

Quantum Interference

Quantum interference is a fundamental phenomenon in quantum mechanics that arises from the wave-like nature of quantum particles. In classical physics, waves can interfere constructively or destructively when they overlap, creating patterns of high and low intensity. Similarly, in quantum mechanics, the probability amplitudes of quantum states can interfere, leading to counterintuitive effects that have no classical analog. This interference occurs in the complex probability amplitudes associated with quantum states, not just in their probabilities. Mathematically, if a quantum system can reach a final state through multiple paths, the probability amplitude for that final state is the sum of the amplitudes for each path: ψ_final = ψ_path1 + ψ_path2 + .... The probability of observing this final state is then |ψ_final|², which can lead to surprising results due to cross-terms in the calculation, including the possibility of destructive interference where certain outcomes become impossible.

In quantum computing, interference plays a crucial role in many algorithms, serving as a key mechanism for enhancing the probability of desired outcomes while suppressing unwanted ones. The quantum Fourier transform (QFT), a fundamental building block of many quantum algorithms, relies heavily on quantum interference to efficiently perform operations that would be computationally expensive classically. In Shor's factoring algorithm, interference is used to extract the period of a function, which is key to its exponential speedup over classical factoring methods. Similarly, Grover's search algorithm uses a technique called amplitude amplification, where interference is repeatedly applied to amplify the amplitude of the desired search state. The famous double-slit experiment with single particles beautifully demonstrates quantum interference, showing how individual particles can interfere with themselves, producing a wave-like pattern over many trials. Understanding and harnessing quantum interference is essential for designing effective quantum algorithms and for interpreting the behavior of quantum systems in general.

Key Quantum Algorithms

Quantum algorithms form the backbone of quantum computing, leveraging quantum mechanical phenomena to solve certain problems more efficiently than classical algorithms. Among the most prominent is Shor's algorithm, developed by Peter Shor in 1994, which can factor large numbers exponentially faster than the best known classical algorithms. This poses a significant threat to current RSA encryption systems, spurring research in post-quantum cryptography. Another cornerstone is Grover's algorithm, invented by Lov Grover in 1996, which provides a quadratic speedup for unstructured search problems. While not as dramatic as Shor's exponential speedup, Grover's algorithm has broad applications in database searching, optimization, and cryptanalysis. The Quantum Fourier Transform (QFT) is a fundamental building block in many quantum algorithms, including Shor's, offering an exponentially faster implementation of the discrete Fourier transform

More recent developments include the Quantum Approximate Optimization Algorithm (QAOA) and the Variational Quantum Eigensolver (VQE), which are hybrid quantum-classical algorithms designed for near-term quantum hardware. QAOA aims to solve combinatorial optimization problems and has potential applications in fields like finance and logistics. VQE is particularly promising for quantum chemistry simulations, allowing for the calculation of molecular ground state energies more efficiently than classical methods. The HHL algorithm, named after its inventors Harrow, Hassidim, and Lloyd, offers exponential speedup for solving linear systems of equations, with potential applications in machine learning and data analysis. Quantum walk algorithms provide a quantum counterpart to classical random walks, showing speedups for certain graph problems and search tasks. As quantum hardware continues to advance, these algorithms and newly developed ones promise to unlock the full potential of quantum computing, potentially revolutionizing fields from cryptography and optimization to materials science and drug discovery.

Quantum Hardware Platforms

The race to build practical quantum computers has led to the development of several competing hardware platforms, each with its own advantages and challenges. Superconducting qubits, used by tech giants like IBM, Google, and Rigetti, are currently the most mature technology. These qubits are based on Josephson junctions and operate at extremely low temperatures (near absolute zero). They offer fast gate operations and have demonstrated the ability to scale up to systems with 50-100 qubits. However, they suffer from relatively short coherence times and are sensitive to environmental noise. Trapped ion qubits, championed by IonQ and Honeywell, use individual atoms held in electromagnetic fields as qubits. They boast long coherence times and high-fidelity operations but are generally slower than superconducting qubits and face challenges in scaling up to large numbers of qubits. Photonic quantum computers, developed by companies like PsiQuantum and Xanadu, use particles of light as qubits. They can operate at room temperature and are naturally suited for quantum communication applications, but face difficulties in implementing certain types of quantum gates.

Other promising platforms include topological qubits, which Microsoft is pursuing. These theoretical qubits would be inherently protected from decoherence, potentially offering a more stable platform for quantum computation, but they have yet to be conclusively demonstrated experimentally. Neutral atom qubits, developed by companies like ColdQuanta, use individual neutral atoms trapped in optical lattices. They offer a good balance of coherence time and scalability but face challenges in implementing high-fidelity multi-qubit gates. Spin qubits in semiconductors, pursued by Intel and various research institutions, leverage existing semiconductor manufacturing techniques and could potentially operate at higher temperatures than superconducting qubits, but are currently limited in scale. Diamond nitrogen-vacancy (NV) centers represent another intriguing platform, with potential applications in both quantum computing and sensing. Each of these platforms is at a different stage of development, with researchers working to improve qubit quality, increase the number of qubits, and develop error correction techniques. The ultimate goal is to achieve fault-tolerant quantum computation, where quantum error correction allows for arbitrarily long computations. While it's unclear which platform (or combination of platforms) will ultimately prove most successful, the diversity of approaches provides multiple paths toward practical quantum computers.

Quantum Error Correction

Quantum Error Correction (QEC) is a critical component in the development of large-scale, fault-tolerant quantum computers. Unlike classical bits, quantum states are extremely fragile and susceptible to errors caused by environmental interactions, a phenomenon known as decoherence. These errors can take the form of bit flips (|0⟩ ↔ |1⟩) or phase flips (|+⟩ ↔ |-⟩), or a combination of both. The challenge in quantum error correction lies in the fact that we cannot simply copy quantum information due to the no-cloning theorem, and measuring a qubit to check for errors would destroy its quantum state. To overcome these obstacles, QEC schemes typically encode a single logical qubit across multiple physical qubits. The simplest example is the three-qubit bit flip code, where |0⟩_L = |000⟩ and |1⟩_L = |111⟩. By measuring the parity of pairs of qubits (known as syndrome measurements), errors can be detected and corrected without directly measuring the encoded quantum state, thus preserving the quantum information.

More sophisticated QEC codes have been developed to handle both bit and phase flips simultaneously. The Shor code, which uses nine qubits to encode one logical qubit, was one of the first to achieve this. However, the most promising approaches for practical quantum computing are surface codes and topological codes. These codes arrange qubits in a two-dimensional lattice and perform local syndrome measurements, making them more feasible to implement on near-term quantum hardware. The goal of QEC is to achieve a fault-tolerant threshold, where adding more physical qubits per logical qubit reduces the logical error rate exponentially. Current estimates suggest that between 1,000 to 10,000 physical qubits may be needed for each logical qubit to achieve fault-tolerance, highlighting the significant scaling challenges ahead. Active areas of research in QEC include developing codes with better encoding rates, designing hardware-efficient error correction schemes, and exploring machine learning techniques for decoding error syndromes. As quantum hardware continues to improve in terms of qubit count and quality, implementing effective quantum error correction will be crucial in realizing the full potential of quantum computing for solving complex, real-world problems.

Why These Use Cases Matter

The quantum computing use cases presented here are not merely academic exercises or futuristic speculations; they represent the vanguard of a technological revolution that promises to transform numerous industries and scientific fields. These applications address some of the most pressing challenges and complex problems facing our world today, problems that have long remained intractable using classical computing methods. In finance, quantum algorithms for portfolio optimization and risk analysis have the potential to reshape global markets, offering more stable and efficient economic systems that could benefit billions of people. The pharmaceutical industry stands on the brink of a new era, where quantum simulations of molecular interactions could dramatically accelerate drug discovery, potentially saving countless lives by bringing new treatments to market faster and at lower cost. In the realm of climate science, quantum-enhanced climate models offer the promise of more accurate long-term predictions, crucial for informing policy decisions and mitigation strategies in the face of global climate change.

Moreover, these use cases demonstrate the broad applicability of quantum computing across diverse sectors, highlighting its potential as a general-purpose technology that could drive innovation and economic growth on a scale comparable to the classical computer revolution. The optimization capabilities of quantum computers could lead to more efficient logistics and supply chain management, reducing waste and environmental impact while improving service delivery worldwide. In materials science, quantum simulations could facilitate the discovery of new materials with extraordinary properties, potentially leading to breakthroughs in energy storage, superconductivity, and other fields that could revolutionize our technological infrastructure. The implications for cybersecurity are profound, with quantum technologies both posing challenges to current encryption methods and offering new, theoretically unbreakable encryption techniques. As quantum machines grow more powerful, they could also transform artificial intelligence and machine learning, potentially leading to AI systems capable of tackling complex problems in ways that surpass human capabilities. By exploring and developing these use cases now, we are laying the groundwork for a quantum-powered future, one that could offer solutions to some of humanity's greatest challenges and open up new frontiers of scientific discovery and technological innovation.

What You'll Discover

As you explore our curated selection of quantum computing use cases, you'll embark on a journey through the cutting edge of computational technology and its real-world applications. Each use case is a window into the transformative potential of quantum computing, offering deep insights into how this revolutionary technology is poised to reshape industries and scientific endeavors. You'll discover the specific challenges that have long plagued fields such as finance, drug discovery, cryptography, and climate modeling, and how quantum approaches offer novel solutions to these persistent problems. Our detailed breakdowns will illuminate the quantum algorithms and hardware being employed, from Shor's algorithm for cryptography to variational quantum eigensolvers for chemistry simulations. You'll gain an understanding of how quantum superposition and entanglement are harnessed to perform calculations that would be infeasible for classical computers, and how researchers are overcoming the significant hurdles of quantum decoherence and error correction.

Furthermore, you'll uncover the tangible results and improvements that quantum computing is already achieving in various sectors. From optimizing financial portfolios with unprecedented efficiency to accelerating the discovery of new pharmaceutical compounds, you'll see concrete examples of quantum advantage. The use cases will also provide a glimpse into the future, exploring the potential long-term impacts of quantum computing on global challenges like climate change and energy production. You'll learn about the current limitations of quantum technology and the roadmap for overcoming these obstacles, giving you a realistic view of both the present capabilities and future potential of quantum computers. By examining the implementation details of each use case, including the specific quantum hardware and algorithms utilized, you'll gain practical insights into how quantum solutions are developed and deployed. This knowledge will not only deepen your understanding of quantum computing but also equip you with the insights needed to envision potential applications in your own field of interest or expertise.

Navigating the Quantum Landscape

As you embark on your journey through the quantum computing landscape, you'll encounter a terrain that is both fascinating and complex. The use cases presented here serve as your guide, illuminating the path through this revolutionary field. To navigate effectively, it's crucial to approach each use case with both curiosity and critical thinking. Start by familiarizing yourself with the fundamental concepts of quantum computing – superposition, entanglement, and quantum interference – as these form the bedrock of quantum advantage. As you explore each use case, pay attention to how these principles are applied to solve real-world problems. You'll notice patterns emerging across different applications, such as the use of quantum algorithms like Shor's for cryptography or variational quantum eigensolvers for chemistry simulations. Don't be intimidated by the technical details; instead, focus on understanding the core problem each use case addresses and how quantum computing offers a unique solution. Compare the quantum approaches with classical methods to appreciate the potential speedups and enhanced capabilities that quantum computing brings to the table.

As you progress, you'll find yourself navigating through various industries and scientific domains, from finance and pharmaceuticals to climate modeling and artificial intelligence. Each use case offers a unique perspective on how quantum computing is reshaping these fields. Take note of the current limitations and challenges mentioned in each case, as these provide insight into the ongoing development of quantum technologies. Pay attention to the different quantum hardware platforms discussed, such as superconducting qubits, trapped ions, and photonic systems, to understand the diverse approaches to building quantum computers. As you delve deeper, you'll begin to see the interconnections between different use cases and how advancements in one area can impact others. Don't hesitate to revisit earlier use cases as you gain more knowledge – you'll likely find new layers of understanding with each pass. Remember that the quantum landscape is rapidly evolving, so consider these use cases as snapshots of the current state of the art, with the potential for significant advancements in the near future. By actively engaging with these use cases, asking questions, and drawing connections, you'll not only gain a comprehensive understanding of the quantum computing landscape but also develop the skills to envision new applications and possibilities in this groundbreaking field.